Both models just described have been utilized to predict composite properties of a broad class of materials. The basic model has been used to define unique characteristics of materials having four or more fiber orientation directions. The degraded property model has been used to predict the behavior of CC composite materials.
Material modeling of CC composites is a complex task. The choice of the appropriate analytical code for the prediction of material properties is only an initial step in the material modeling process. Definition of the appropriate modeling parameters must be determined so that the best material representation is created. The required modeling parameters are analytical code dependent an may include such things as fiber and matrix properties, degree of matrix cracking, and fiber bundle sheath content. Definition of these parameters is most appropriately obtained through extensive data correlations.
Prior to initiating a data correlation study, a thorough understanding of the history of the material is necessary. Not only is a definition of the weave architecture and types of constituents that comprise the material required, but also a concise understanding of the process history must be known as well. Fibers utilized in fabrication undergo property changes due to the high-temperature heating cycles occurring in the CC process. These property changes are dependent on the type of fiber and they vary based upon the maximum process temperature. For example, the process temperature may result in an increased stiffness for the fiber while degrading its strength.
The effective properties of the matrix material are very much affected by the process procedure. These effects can
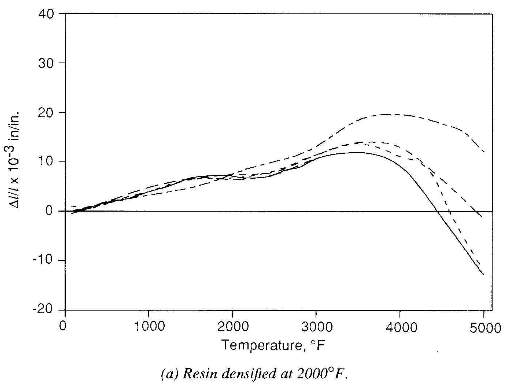
resin densified at 2000F
be observed in figure 6. Figure 6 shows the measured composite thermal expansion response for two 2D CC materials that have been subjected to different densification procedures. The densification process caused the impregnant to undergo various phase changes.
The process history is also important in characterizing other factors. The processing of CC materials may result in a final composite that can contain a significant amount of matrix microcracking. This microcracking results from cooling the densified material to room temperature. The degree of cracks in the material is related to the final process temperature of the composite. Matrix microcracking affects the matrix-dominated properties of the composite, which include shear and thermal expansion. The use of thermal
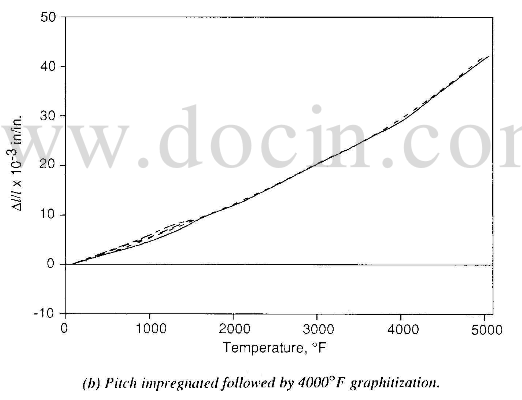
pitch impregnated followed by 4000F graphitization
expansion and shear data can help quantify the degree of cracking in the material. For example, by utilizing the DCAP code, an estimate of the amount of matrix microcracking can be accomplished by correlating expansion data with values of the DCAP unit cell efficiency parameter S.
Another important factor is the method of impregnation. For example, an initial pitch impregnation cycle will cause a sheath of highly orientated matrix material to form around the fiber bundles. This sheath of high modulus matrix material acts to increase the stiffness of the bundles. The use of fiber direction composite tensile modulus measurements helps define the amount of sheath present.
A primary requirement for the accurate modeling of CC materials is the determination of fiber and matrix properties. Associating the correct representation of fiber and matrix properties with particular process methods is vital in the modeling of these complex materials; therefore, it is important that the processing history of the material be factored into material property modeling and that the appropriate material representation be formulated.
The verification of the fiber and matrix properties can be accomplished through correlation of experimental data with predicted properties. Through the use of data correlation, an appropriate material model can be defined for use in the efficient design of these materials. Differences between the predicted and measured behavior of materials are used to improve the understanding of both the constituents and the interactions between the components of the composite.
The determination of the properties of the transversely isotropic fiber is a bit more complex. The initial step is to define the fiber axial modulus. This determination is accomplished through correlation of fiber direction composite data. Effective fiber axial modulus can be backed out from experimental data through the use of the rule of mixtures. Comparisons can then be made to known properties of similar fibers to enable the determination of temperature effectiveness.
The use of available data on the relationships of fiber properties is utilized as a tool to approximate the other required fiber constants.
The determination of the necessary parameters utilized in the prediction of effective composite properties is an iterative procedure. For example, revised approximations to fiber modulus may change the estimated amount fiber bundle sheath which may present in the material. The degree of approximated matrix microcracking may not be compatible with the effective matrix properties. Data correlations must be performed, with options available, to continually update all necessary material model parameters. In addition to this the engineer must carefully scrutinize the processed material to determine if the specifications of weave architecture have been met because deviations in bundle orientation can result in unexpected material response.