In the present application, the rate constant ranges between 10-1 and 200 m/s, the diffusion coefficient is close to 10-4 m2/s, and, taking Iμ as a reference length, the dimensionless numbers take approximately the following values: Pe=500, Da ∈[10-2, 20], w=3*10-4. The proposed range for the Damkohler number is due to the range on the pre-exponential factor, Ks, defined in Eq.(1).
The obtained value of the Peclet number suggests that, even at the micro-scale, mass transfer is dominated by advection. However, in a recent study of the effective reaction rate for a rough surface, it has been shown that the effective reaction rate is not sensitive upon the Peclet number below a value about Pe=500, for a wide range of Damkohler numbers. This indicates that a purely diffusive analysis has a relatively broad applicability range.
The condensation ratio shows that recession is slow compared to reaction. Moreover as w/Da<1, recession is slow compared to diffusion relaxation. The diffusion-reaction process is not influenced by the recessive displaycement of the surface and velocity in the local frame can be identified with the velocity in the frame linked to a non recessive surface.
In a first approach, we will assume that the Peclet and the condensation numbers are small, i.e., we neglect advection effects, and the obtained model can be written:
аc/аt -D△c=o in Ω (2)
n.(-D∇)- kc =o on ∑ (3)
v + kc/cs n=o on ∑ (4)
Eq. (2) is a pure transient diffusion equation describing the reactant transport in the volume above the surface, Eq. (3) describes the matching of the incoming reactant flux and of the heterogeneous reaction rate at the surface, and Eq. (4) describes the surface recession with v being the surface velocity. This is comparable to the model conditions derived for the study of ablative thermal protection system C/C components. However there will be a difference when applying this model to the large scale evolution of the materials, as shown later.
Numerical approach for the recession model:
The problem for the recessive model requires the description of a moving interface. Interface tracking methods can be divided into two different general approaches. The first idea is to have a Lagrangian tracking of the interface. In this technique, the velocity of each node of the interface is computed and the geometry is rebuilt at each time step. Such a method can be used in a classical finite element procedure. Nevertheless, the geometry actualization and the associated re-meshing contribute to a high CPU time. The second method is a Eulerian description of the interface. In this method the problem which is written for each phase is transformed into a continuous formulation valid everywhere in the computed domain. In this class of method, different possibilities are available, such as the Volume of Fluid method, level-set approaches, and many other phase-field approximations.
Description of the method:
This work makes the use of the VOF method, featuring a Piecewise Linear Interface Calculation (PLIC) because of its ability to work with non-differentiable surfaces. Indeed, the major difficulty for the problem under consideration lies in the description of the interface. The micro-scale observation of the ablated meterial shows that albation leads to sharp edges.
In the PLIC description, the interface is modeled by local planar surface, whose positions and slopes are obtained from the phase indicator variable, as illustrated in Fig.3. We adapted this technique to our problem with the idea to keep the possibility of sharp edges, as it is a characteristic feature of ablated surfaces. We do not describe here the details of the numerical technique, since it involves a fastidious listing of all possible geometrical situations.
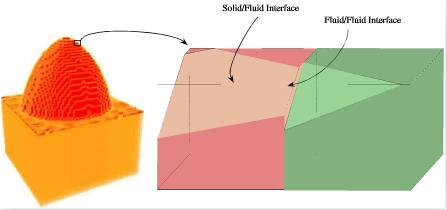
fig.3-interface-description-at-the-voxel-scale