The modelling of ablation of carbon/carbon (C/C) composite utilized as rocket engine hot parts is addressed under the angle of the competition between bulk transport of reactants and heterogeneous mass transfer, associated to reactivity contracsts between constituent phases. A numerical solver based on a simple model and built on a VOF technique allows direct simulation at two scales. Its application to actual complex materials is performed; the results are consistent with experimental data and help understanding the origin of the material behaviour, either in terms of acquired surface morphology or in terms of effective recession rate.
In the high-technology field of rocket solid propulsion, for example in the case of Ariane V boosters, thermal protection materials constituting the nozzle and divergent inner walls are submitted to very high temperatures- up to 3000K. Under such heavy solicitations, few materials can remain in the solid state. Among them, C/C composites have several relative advantages: excellent ratio of mechanical properties versus density at high temperature, small thermal expansion, cost-effective processing of thick and large parts.
In spite of these performance, the thermochemical constraints lead to a recessive degradation of the C/C composite surface by mass loss or ablation. The causes of this mass loss is mainly oxidation, while mechanical erosion may also play a role.
The ablation of the composite walls acts at a macroscopic scale and modifies the device geometry: the throat secton increases. This may lead to a thrust loss compared to the nominal performances of the propulsion system. Moreover, as the thickness of the parts is reduced, the insulating function of the composite is damaged and may lead to a degradation of bonding parts. This macroscopic change in the geometry is linked to a modification of the microscopic structure of the composite characterized by an increase of the surface roughness. Indeed, the surface acquires a multiscale roughness which has been observed using SEM microscopy as illustrated in (5,6). It is also reported in {1} that this roughness development leads to an increase by a factor 1.7 of the convective heat flux received by the composite, which in turn has an impact on the recession velocity. These observations illustrate the fact that ablation is a multiscale and multiphysics process involving strong couplings between recession, surrounding flow, heat and mass transfer.
Many experimental characterizations of ablative materials have been reported; they usually consist in SEM observations of the ablated surfaces as well as of recession rate measurements. Usual patterns of the rough surfaces are fiver denudation at the micro-scale, due to a weak interphase or a weak matrix, and block denudation at macro-scale, mainly due to mechanical erosion of poorly bonded parts of the composite.
Numerous modelling studies have focused on the surrounding fluid behavior with very simple descriptions of the composite properties. On the other hand, studies dealing with the structural and chemical complexity of such materials do not take into account the transfer/ recession coupling. The different points of view adopted in these works correspond to the fact that the composite heterogeneity and the global flow have different scales. The surrounding flow must be known at the part-scale, i.e., a metric scale, whereas the composite is heterogeneous at a micrometer scale as illustrated by FIg.1. Therefore, the composite properties must be up-scaled in order to obtain an effective composite description suitable for macro-scale simulations.
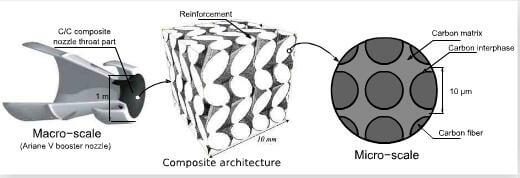
fig-1-multiscale-structure-of-C-C-composites-used-as-nozzle-throat-parts.
In this paper, the focus is set on the competition between mass transfer and recession of the composite surface, with the objective of building an equivalent or effective macro-scale model yielding both a correct surface morphology and an adequate recession rate.
The document is organized as follows. In a first section, a description is given of the physico-chemical model that has to be modelled. Then, the model is set up, making use of some assumptions. A numerical method is outlined in a third part. Finally, its applications to two actual cases are described and discussed.