Johnson has suggested that the tensile failure of carbon fibers is due to the presence of defects and the structure suggests that anisotropic effects may be ignored and the size of the basal plane cracks estimated from a simple Griffith relation:
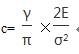
Where γ=surface free energy
c=size of the basal plane cracks
Cottrell has estimated the value of the surface free energy as 4.2 Jm-2. Hence Reynolds has drawn curves of defect size vs fiber strength for Type Ⅰand Type Ⅱ fibers, indicating the size of the defect which has to be eliminated to obtain a given strength.
Goggin examined the strengths of three samples of Type Ⅱ carbon fiber produced from the same feedstock and showed that they converged to an intrinsic fiber strength of 6.5-7.0 Gpa at 0.1 mm gage length.
Coleman showed that the strength of a tow of fibers will be less than the mean fiber strength as determined b the number of low strength fibers, effectively reducing the tow cross-section and is related to the strength dispersion,
![]()
Which was typically 0.2 at a 5 mm gage length, suggesting a maximum tow strength of some 70% of the mean
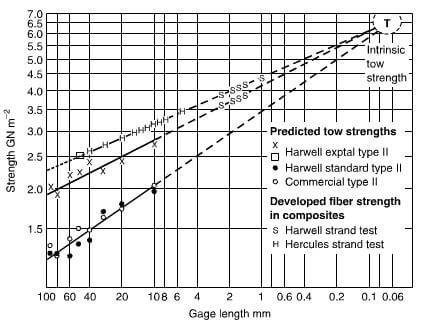
fig.20.13-predicted tow strengths and effective gage lengths in composites.
filament strength at this gage length. By applying correction factors to the figures in Figure 20.8, Hughes and Jackson predicted the intrinsic tow strength at this gage length to be about 6.5 Gpa, as shown in Figure 20.13. Hughes et al used a gage length of 3mm and obtained an estimated strength up to 5 Gpa, whilst Jones and Johnson used a loop method and obtained an estimated strength of 7 Gpa and Tsushima used a knotted loop method and reported 6 Gpa.
There are three factors which are particularly important in controlling the strength of composites, apart from the basic fiber and matrix properties namely:
- Critical length
- The fiber volume fraction
- The alignment of the fiber
The tensile properties of carbon fibers have been investigated. Tibbets et al determined the properties of VGCF.