The basic mini-mechanical material model proposed for multidirectional reinforced composite materials is based upon the concept that a composite material system can be regarded as assemblage of unit cells. This fact is illustrated in figure 3. The basic unit cell is defined by fiber and matrix properties and the phase geometry. The effective property analysis is performed on the representative volume element which contains a large number of unit cells. The material variability can be incorporated by treating an assemblage of RVE’s having some statistical variability of, for example, fiber volume fraction.
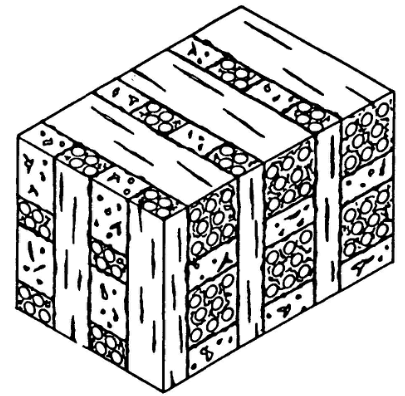
section of 3D orthogonally reinforced mateiral showing assembly of unit cells
The unit cell models are constructed from impregnate yarn bundles oriented in space and from interstitial matrix regions as shown schematically in figure 3. Several basic versions of this unit cell model have been analyzed. To be effective, a model of the material must include the following material characteristics:
- Anisotropic constituents, including the effects of oriented matrix material such as in a fiber “sheath”
- Definition of fiber content within each fiber bundle, as well as definition of total fiber content within a repeating element.
- Definition of orientation of each fiber bundle within a repeating element.
- Definition of the interface properties between subcell regions to model the subcell cracking that exists in most CC materials.
- Dispersed voids, of both random and elongated shapes
- Temperature-dependent constituent properties
The MSC NDPROP (N-directional composite analysis program) model has been developed for the analysis of very general composite unit cells. The unit cell is composed of fiber bundles oriented in space by defining direction numbers that determine the orientation of each fiber bundle. The cell can contain any number of bundles, provided that the total bundle and interstitial matrix volume fractions do not exceed unity. The material does not need to be orthotropic, but can be fully anisotropic, if necessary. Each of the fiber materials can be different, thus allowing treatment of hybrid composites. The constituent fiber and matrix materials may have transversely isotropic elastic constants and thermal expansion coefficients. Material porosity can be treated and matrix properties in each fiber bundle and in the interstitial matrix regions can differ.
The deficiency in the NDPROP model is the lack of ability to model explicitly the interface regions between bundles. Rather, an effective matrix is defined which includes the effects of cracks between bundles.
The DCAP (directional composite analysis program) model, which was developed under U.S. Navy funding and is available to qualified government contractors through the Naval surface weapons center, focuses on the effects of the significant localized microcracking that occurs in CC composites. This model considers a unit cell that is reinforced with three locally orthogonal fiber bundles and which contains regions of material with variable stiffness between the unit cell subregions. Actual crack geometry and crack-tip stress intensity effects are not considered. Rather, the transmission of loads across the interface in the unit cell is considered. This approach to the effect of mirocracking leads to a definition of the efficiency of the unit cell interfaces in transmitting loads. The nuit cell efficiency can be considered equivalently as either the transmission of a load, or as a measure of the uncracked contact area along the interfaces within the unit cell.
The drawback with the DCAP model is that it is developed especially for three directionally reinforced materials and can’t handle multidirectional materials or thin 2D material easily. Multidirectionally reinforced materials require an analysis approach similar to NDPROP, which assumes an effective matrix material. Thin-section 2D laminated-type materials can be analyzed with a laminate analysis code, as described in the following sections.